SEE++ implementiert sowohl die rein geometrischen Modelle (Faden- und Bändermodell) als auch die kinematischen Modelle mit geometrischen Komponenten (SEE-KID Modell, SEE-KID Active Pulley Modell und Orbitmodell). Dabei werden grundsätzlich Richtlinien für Koordinatensysteme und Beschreibungen von Augenpositionen und Rotationen verwendet, welche wiederum aus der Historie der Augenforschung stammen.

Einer der ersten Versuche, um ein besseres Verständnis für Augenmotorik zu erlangen, waren die so genannten Ophthalmotrope. Ruete konstruierte 1845 ein mechanisches Modell des menschlichen Auges aus Holz und Fäden, um den Augenbewegungen zu Grunde liegende Gesetzmäßigkeiten besser untersuchen zu können. F.C. Donders stellte 1848 das Donders'sche Gesetz auf: Fixiert ein Auge einen Gegenstand im Raum, so wird durch die Position des Gegenstandes auch die Augenposition definiert. Ferner wird die Verdrehung des Bulbus um die Sichtachse (Torsion) auch abhängig von dieser Augenposition eindeutig beschrieben.

 

Halle's und Ruete's Ophthalmotrop [Simonsz und Tonkelaar, 1990]

 

Als die deutsche Ausgabe der Publikation von Donders erschien, erregte dies die Aufmerksamkeit von H. Helmholtz, der wiederum eine Erklärung für die von Donders gefundene Torsion in Abhängigkeit von der Augenposition fand. Er bezeichnete diese torsionale Verdrehung des Bulbus als "Pseudotorsion", welche als Messfehler zustande kommt, aber nicht wirklich existiert. Pseudotorsion ist jener Effekt, der bei der Messung von Augenposition in tertiären Blickrichtungen den horizontalen sowie den vertikalen Meridian durch das Auge in Bezug auf eine vertikale Linie im Umgebungsblickfeld, verdreht. Der Grund dafür ist, dass die Meridiane (Kreuz auf der Cornea in SEE++) in einem bulbusfixen Koordinatensystem definiert sind.

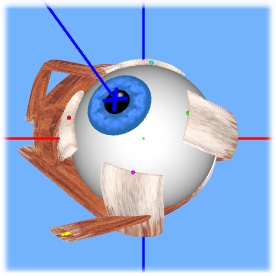
Pseudotorsion in tertiärer Blickposition

 

Nachdem Pseudotorsion durch eine unpassende Wahl des Koordinatensystems zustande kommt, hatte J.B. Listing um 1853 die Idee, ein Polarkoordinatensystem zu verwenden. Dabei entdeckte er auch, dass alle tertiären Augenpositionen, ausgehend von der Primärposition, durch die Rotation um eine bestimmte Achse erreicht werden konnten, und weiters, dass alle diese Rotationsachsen in einer Ebene enthalten sind (Listing'sche Ebene), wobei der Winkel der torsionalen Verdrehung konstant ist. Diese Entdeckung wurde dann als Listing'sches Gesetz bezeichnet. Das Listing'sche Gesetz beschreibt damit den torsionalen Winkel in einer bestimmten Augenposition immer gleich, unabhängig wie diese Blickposition erreicht wurde.

 

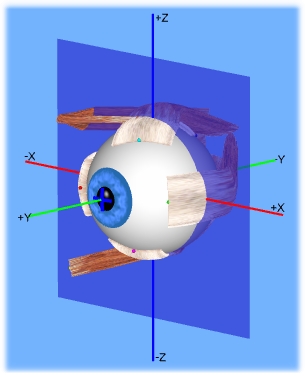
Die Listing'sche Ebene eines gesunden linken Auges

 

Wie bereits erwähnt kann also die Listing'sche Ebene durch die Darstellung der Endpunkte der Rotationsachsen, die eine 3D Augenposition ausgehend von der Primärposition in eine beliebige andere Augenposition beschreiben, charakterisiert werden. Bei einem gesunden Auge steht diese Ebene parallel zur X-Z Ebene des Koordinatensystems (siehe Abbildung), wobei bei einem pathologischen Auge die Ebene entsprechend der torsionellen Effekte der jeweiligen Pathologie verkippt. In der 3D-Ansicht von SEE++ kann die Listing'sche Ebene entsprechend der aktuell simulierten Pathologie eingezeichnet werden.

Als Donders' Gesetz und das Listing'sche Gesetz publiziert wurden, stellte sich sofort die Frage nach einer einheitlichen Definition der Abfolge der Rotationen um die einzelnen Koordinatenachsen für die Beschreibung von Augenpositionen.

 

Geometrische Beschreibung von Augenpositionen

Auf Grund der Nicht-Kommutativität von Rotationen im 3D-Raum ist es notwendig, eine einheitliche Reihenfolge der Beschreibung von Augenposition zu verwenden bzw. bei einer Augenposition, beschrieben durch drei Komponentenwinkel, auch die verwendete Rotationsreihenfolge anzugeben. A. Fick definierte 1854 die so genannte Fick-Winkelreihenfolge, wobei die Rotationsreihenfolge zuerst um die vertikale Achse, dann um die horizontale und schließlich um die torsionale Achse zu erfolgen hat. Im Gegensatz dazu definierte Helmholtz die Rotationsreihenfolge zuerst um die horizontale, danach um die vertikale und torsionale Achse. Beide Systeme der Rotation beschreiben eine kardanische Aufhängung des Bulbus unter Berücksichtigung der jeweiligen Rotationsreihenfolge. Aus der Darstellung der beiden Systeme (siehe nachfolgende Abbildung) ist leicht zu erkennen, dass ein und dieselben Winkel als Definition einer Augenposition in beiden Systemen zu unterschiedlichen Stellungen des Bulbus und somit unterschiedlichen Augenpositionen führen.

 

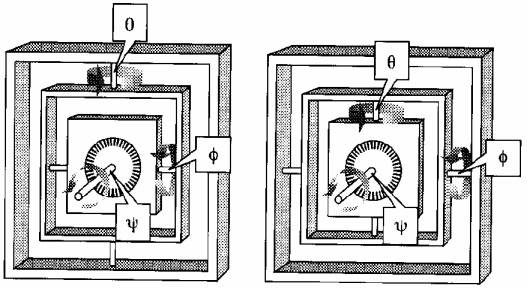
Kardanische Aufhängung nach Fick (links) und Helmholtz (rechts)

 

Das SEE++ System verwendet generell die Rotationsdarstellung nach Fick, womit eine Augenposition in drei Winkel, zuerst um die vertikale Achse, dann um die horizontale Achse und letztlich um die torsionale Achse beschrieben wird.

 

Für die komplette Definition von Augenpositionen ist zusätzlich das verwendete Koordinatensystem von Bedeutung. In nachfolgender Abbildung sind die Koordinatenachsen, deren Vorzeichen und Richtungen für beide Augen dargestellt.

 

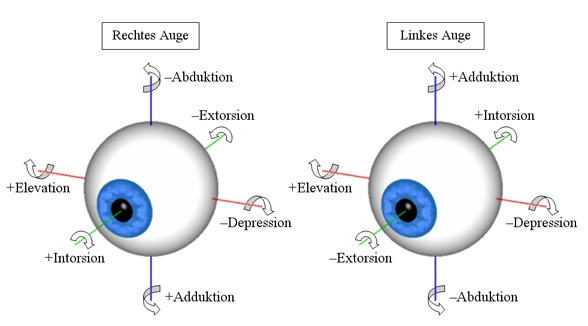
Die sechs möglichen Rotationsrichtungen der Augen

 

Das für die Extorsion verwendete Koordinatensystem ist für beide Augen bezüglich der Ab-/Adduktions und In-/Extorsionsachse verschieden. Die Drehrichtungen um die jeweiligen Achsen können wie folgt beschrieben werden (die Nase ist in obiger Abbildung zwischen den beiden Augen anzunehmen):

 

1. Rotation um Z-Achse (Duktion, blau)

 positiver Winkel = Adduktion (zur Nase hin)

 negativer Winkel = Abduktion (von der Nase weg)

 

2. Rotation um X-Achse (Elevation, rot)

 positiver Winkel = Elevation (nach oben)

 negativer Winkel = Depression (nach unten)

 

3. Rotation um Y-Achse (Torsion, grün)

 positiver Winkel = Intorsion (Einwärtsrollung)

 negativer Winkel = Extorsion (Auswärtsrollung)

 

Wie aus obiger Abbildung ersichtlich ist, sind die Koordinatenachsen für Ab-/Adduktion und In-/Extorsion in beiden Augen mit unterschiedlichen Vorzeichen definiert. Dies ermöglicht die einheitliche Definition der Winkelrichtung mit gleichzeitiger Bezeichnung (z.B.: Abduktion = von der Nase weg). In beiden Augen ist weiters die Rollung um die Blickachse nach innen mit einem positiven Vorzeichen definiert. Würden die beiden Achsen nicht unterschiedliche Vorzeichen aufweisen, so würde bei beidseitiger Intorsion ein Auge nach außen rollen und eines nach innen. Die Elevations-/Depressionsachse bleibt in beiden Augen gleich, da die auf- und abwärts-Bewegungen in beiden Augen die gleichen Richtungen aufweisen.

 

Zusätzlich anzumerken sei jene Situation der binokularen Augenbewegung, bei der bei Abduktion des einen Auges eine Adduktion des anderen Auges erfolgen muss, also die Augenpositionen hinsichtlich Ab-/Adduktion und In-/Extorsion gespiegelt werden müssen.

 

Bulbus Translation

Das Auge ist in der Orbita umgeben von elastischen Fettpolstern, die, neben der eigentlichen Rotation, auch eine Translation des Bulbus bis zu einem gewissen Grad erlauben. Meist ist diese Translation vernachlässigbar gering, denkt man aber an einige pathologische Situationen der Co-Kontraktion von Muskeln (z.B. Duane Syndrom), so wird diese zusätzliche Bewegung des Bulbus zu einem wichtigen Anhaltspunkt für die Abschätzung und Korrektur einer Motilitätsstörung. Das SEE++ System berechnet auf Wunsch diese Bulbus Translation und zeigt diese in der 3D-Darstellung an, wobei eine Vorwärtsbewegung des Bulbus in Richtung der Y-Achse als Protrusion (Bulbus Translation mit positivem Vorzeichen) und eine Rückwärtsbewegung in Richtung Orbitaspitze als Retraktion (Bulbus Translation mit negativem Vorzeichen) bezeichnet wird. Die jeweiligen Werte für Protrusion und Retraktion sind im System für jede Augenposition textuell ersichtlich. In der 3D-Ansicht kann die Bulbustranslation auch eingezeichnet werden.

 

Geometrische Beschreibung der Muskelwirkung

Um die geometrische Definition des extraokulären Augapparates zu vervollständigen, benötigt man auch die geometrische Beschreibung der am Bulbus ansetzenden Muskeln und deren Wirkungsrichtungen. Die geometrische Beschreibung eines Muskels basiert auf der Definition von wichtigen Anhaltspunkten, während die Muskelwirkungsrichtung über die Definition einer Rotationsachse, um die der Muskel den Bulbus rotieren würde, bestimmt wird. Die Beschreibung eines Muskels wird über die Formulierung eines Muskelpfads vom Ursprung bis zur Insertion aufgestellt. Dabei ist auch zu beachten, wie sich dieser Muskelpfad bei Einnahme verschiedener Blickpositionen verändert bzw. an die Position des Bulbus anpasst.

 

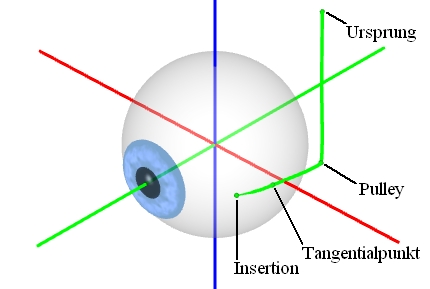
Definition des Muskelpfads

 

 

Die Abbildung zeigt den Pfad des äußeren geraden Muskels (rectus lateralis), definiert durch Muskelursprung, Pulley, Tangentialpunkt und Insertion. Der Muskelursprung liegt im hinteren Bereich der Orbitahöhle im so genannten Annulus Zinnii (Zinn'scher Ring). Der Pulley wirkt als Umlenkrolle und stabilisiert den Muskelpfad im hinteren Orbitabereich. Dieser Punkt wird im Faden- und Bändermodell nicht verwendet, da diese beiden Modelle von einer Definition des Muskelpfads ohne Pulley ausgehen. Der Tangentialpunkt markiert jenen Bereich, an dem der Muskelpfad den Bulbus zu allererst berührt. Die Strecke zwischen Insertion und Tangentialpunkt wird als Abrollstrecke bezeichnet.

 

Die unterschiedlichen Reaktionen des Muskelpfads auf Veränderungen der Blickposition werden von verschiedenen Modellen unterschiedlich repräsentiert. So bestehen wesentliche Unterschiede in der Definition des Muskelpfads zwischen Faden-, Bänder-, Orbit- und SEE-KID Modell. Faden- und Bändermodell verwenden für diese Definition ausschließlich Muskelursprung, Tangentialpunkt und Insertionspunkt, wogegen SEE-KID Modell und Orbitmodell den zusätzlichen Punkt des Pulleys berücksichtigen. Im SEE-KID Active Pulley Modell wird der Pulley schließlich sogar bei Bewegungen des Bulbus mitbewegt.

 

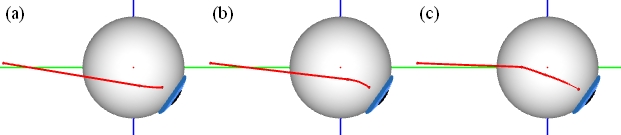
Vergleich von (a) Faden-, (b) Bänder- und (c) SEE-KID Modell

 

Vergleicht man die Muskelpfaddarstellung dieser Modelle (siehe Abbildung), so fällt die unterschiedliche Darstellung der Bewegung des Tangentialpunktes auf. Im Fadenmodell (a) sowie im Bändermodell (b) wird der Tangentialpunkt, und somit auch der gesamte hintere Muskelpfad mit dem Bulbus nach unten gezogen. Dies verändert auch ganz wesentlich die Zugrichtung des Muskels in anderen Blickpositionen. Besser prognostiziert hier das SEE-KID Modell (c). Durch Einführung des Pulleys wird eine Stabilisierung der Wirkungsrichtung des Muskels erreicht, und damit eine wesentlich realistischere Prognose.

 

Die Beschreibung der Rotationsachse eines Muskels, und somit auch der Wirkung des Muskels auf den Bulbus, wird vom Muskelpfad abgeleitet. Während die Rotationsachse im Faden- und Bändermodell normal auf die Ebene von Insertion, Tangentialpunkt und Ursprung steht, wird im Orbitmodell, SEE-KID und SEE-KID Active Pulley Modell zusätzlich der Pulley-Punkt berücksichtigt. Die Wirkungsrichtung (Rotationsachse) eines Muskels lässt sich auch in allen drei Komponenten (x,y,z) aufgeschlüsselt als Diagramm darstellen, um eine bessere Abschätzung der verursachten Rotation zu gewinnen. Die x-Komponente der Rotationsachse repräsentiert den Anteil der Elevation/Depression, die ein Muskel auf den Bulbus ausübt, die y-Komponente gibt Auskunft über Intorsion/Extorsion und die z-Komponente über Abduktion/Adduktion.

 

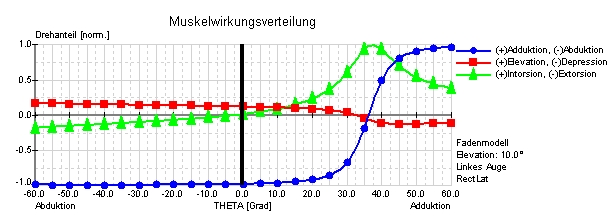
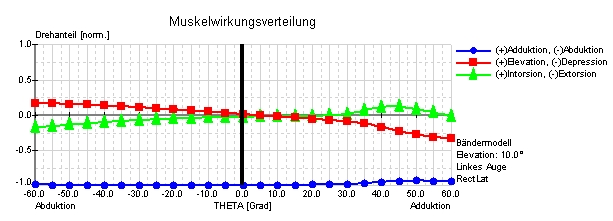
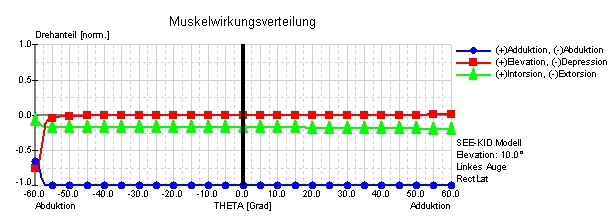
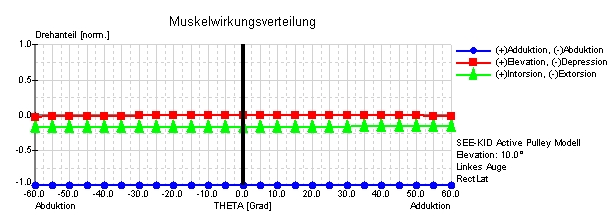
Muskelwirkungsverteilung von Faden-, Bänder-, SEE-KID und SEE-KID Active Pulley Modell des m. rectus lateralis

 

 

Die Muskelwirkungsverteilung stellt die relativen Drehanteile für ausgewählte Augenmuskeln über den horizontalen Blickbereich (siehe Abbildung) in einer bestimmten Elevations-, Depressionsebene dar. Die Drehanteile werden in normierten Werten zwischen –1 und +1 für Ab-/Adduction, Elevation/Depression und In-/Extorsion angegeben. Die Abbildung zeigt die unterschiedliche Wirkungsverteilung des m. rectus lateralis im Faden-, Bänder-, SEE-KID und SEE-KID Active Pulley Modell bei einer Elevation von 10 Grad über dem horizontalen Blickfeld (0.00-Linie in Abbildung) bei bis 60 Grad Ab- und Adduktion eines linken Auges.

 

Klar ersichtlich wird hier die physiologisch fehlerhafte Prognose des Fadenmodells, bei dem der m. rectus lateralis seine abduzierende Hauptwirkung, ab ca. 36 Grad Adduktion, in eine stark adduzierende Wirkung verändert. Der Vergleich mit dem Bändermodell zeigt für exakt dasselbe Szenario durch Beibehaltung der Hauptwirkung des m. rectus lateralis eine wesentlich physiologischere Wirkungsverteilung. Diese Unterschiede entstehen durch die differenzierte mathematische Modellierung der anatomischen Strukturen. Während im Fadenmodell der Muskelpfad im Kontaktbereich mit dem Bulbus durch den kürzesten Weg zwischen Insertion und Ursprung definiert wurde, enthält das Bändermodell eine winkelreduzierende Komponente, die den Muskelpfad durch die Relativbewegung des Tangentialpunktes in Abhängigkeit von der Blickposition beschreibt. Dies ermöglicht die Simulation eines stabilisierenden Bindegewebs- und Halteapparates, um die Bewegung der Muskeln bei steigendem Blickwinkel zu limitieren. Resultierend zeigt sich eine Biegung des Muskelverlaufs zwischen Insertion und Tangentialpunkt, die tendenziell den anatomischen Gegebenheiten wesentlich besser, jedoch nicht optimal, entspricht.

 

Erst durch die Einführung eines Modells, welches auch Pulleys berücksichtigt, können detailliertere Simulationen und pathologische Fallstudien durchgeführt werden. Die mathematische Basis für so ein Modell bildet die Einführung eines zusätzlichen funktionellen Ursprungs (Pulley) unmittelbar hinter dem anatomischen Äquator des Bulbus. Dadurch erfolgt eine Stabilisierung des Muskelpfads im hinteren Orbitabereich, wobei die Definition der Muskelwirkungsrichtung vom funktionellen Ursprung ausgeht. Der anatomische Ursprung ist für die blickpositionsabhängige Wahl der Wirkungsrichtung von mathematisch geringer Bedeutung. Die Simulation von Pulleys im SEE-KID Modell (und auch im Orbitmodell) zeigt in der Muskelwirkungsverteilung eine wesentlich bessere Beibehaltung der Muskelhauptwirkung, jedoch gibt es bei ca. 55 Grad immer noch eine leichte Abweichung der Muskelhauptwirkung. Erst mit der Einführung von "aktiven Pulleys", also Pulleys, die sich entsprechend der gewählten Blickposition mitbewegen (SEE-KID Active Pulley Modell), zeigt die Muskelwirkungsverteilung im gesamten Blickfeld von -60 bis +60 Grad eine vollständige Beibehaltung der Muskelhauptwirkung. Somit ist das SEE-KID Active Pulley Modell als (geometrisches) Modell derzeit am besten geeignet.

 

Funktionelle Topographie

Die funktionelle Topographie erlaubt es, die Muskelwirkungsverteilung für alle möglichen Insertionen eines Muskels als farbcodierte 3D Darstellung auf den Bulbus zu projizieren. Dabei wird die Insertion eines gewählten Muskels "virtuell" an verschiedene Stellen auf dem Bulbus bewegt und bei jeder Insertionsposition werden die verschiedenen Drehanteile (Ab-/Adduktion, Elevation/Depression, In-/Extorsion) als farbcodierte Helligkeitswerte (dunklere Helligkeitswerte entsprechen einem hohen Drehanteil bei Insertion des Muskels an der entsprechenden Stelle) auf dem Bulbus eingezeichnet. Die Zuordnung der Farben zu den entsprechenden Drehanteilen ist dabei gleich wir beim Muskelwirkungsverteilungdiagramm, also blau für die Duktion, rot für die Elevation/Depression und grün für die Torsion. Bei gleichzeitiger Anzeige von mehreren Drehanteilen werden die Farben kombiniert und es ergeben sich entsprechende Mischfarben.

Mit Hilfe dieser Farbcodierung ist es nun möglich, für einen bestimmten Muskel eine "ideale" Muskelansatzlinie zu finden, bei der ein bestimmter Drehanteil entweder minimal (weißer bzw. heller Bereich am Bulbus) oder maximal (dunkler Bereich in der entsprechenden Farbe am Bulbus) sein soll. Durch die kombinierte Darstellung von mehreren Drehanteilen können auch Schnittpunkte gefunden werden, bei denen mehrere Komponenten gleichzeitig minimal oder maximal werden. Diese "idealen" Ansatzlinien und Schnittpunkte in Kombination mit den Polen und den Koordinatenachsen bieten eine wertvolle Hilfestellung bei der Planung von operativen Eingriffen.

In der nachfolgenden Abbildung sieht man die Verteilung der horizontalen Drehanteile (blau) des linken m. obliquus superior in der Primärposition. Dunkelblaue Bereiche stellen mögliche Insertionspositionen dar, bei denen der Muskel das Auge stark in die Ab-/Adduktion ziehen würde, hellblaue oder weiße Regionen hingegen repräsentieren Bereiche, in denen der Muskel nur sehr wenig oder gar nicht in die Ab-/Adduktion ziehen würde. Bei der funktionellen Topographie kann, im Gegensatz zum Muskelwirkungsverteilungdiagramm (MWVD - siehe Definition der Muskelwirkungsverteilung), die Richtung (also ob ein Muskel bei Insertion in einem z.B. blauen Bereich in Adduktion oder in Abduktion ziehen würde) nicht abgelesen werden. Die funktionelle Topographie kann in SEE++ über die Symbolleiste für die 3D-Ansichtsoptionen eingeblendet werden.

 

Funktionelle Topographie des m. obliquus superior (Ab-/Adduktionskomponente, horizontal)

 

Geometrische Vermessung des Auges

Um 1869 wurde von A.W. Volkmann eine statistische Analyse von mehreren Patienten durchgeführt. Diese Ergebnisse wurden dann als Daten für ein so genanntes "Normauge", also ein durchschnittliches Auge eines Menschen, publiziert. Auf den Daten von Volkmann basierend wurden dann auch das Faden- und Bändermodell formuliert. Diese geometrischen Grunddaten wurden dann später von Robinson und Miller noch erweitert, verändert bzw. durch Pulleys ergänzt.

 

Geometrische Daten nach Volkmann

 

Diese geometrischen Daten sind in dem bereits definierten Koordinatensystem (siehe Geometrische Beschreibung von Augenpositionen) anzuwenden. SEE++ bietet auch ein Standard-Szenario, um auf diese Daten von Volkmann zurückzugreifen.

 

Die Entdeckung von Pulleys als funktionelle Elemente 1989 (Miller und Demer) revidierte diese Daten:

 

Geometrische Daten nach Miller und Demer

 

Die Muskelinsertionen sowie die Pulleypositionen wurden hier dreidimensional vermessen. Dies bedeutet, dass mit der geometrischen Abstraktion, den Bulbus als kugelförmiges Objekt anzunehmen, jeder Muskel mit seiner Insertion nicht exakt auf dem Bulbus liegt, weil dieser in der Realität ellipsoid geformt ist. Dies bedeutet gleichzeitig einen "Kompromiss" in der Wahl des Bulbusradius, der sich als kleinster Radius aller sechs Muskeln definiert. Der muskelbezogene Bulbusradius, sowie der "eigentliche" Bulbusradius lassen sich über Parameter in SEE++ jederzeit ändern. Der wesentliche mathematische Unterschied dieser Daten besteht darin, dass nun jeder Muskel seinen eigenen "virtuellen Bulbus" rotiert, was sich wiederum auf den Hebelarm und das Kraftverhalten auswirken kann.