Um ein mechanisches System vollständig simulieren zu können, wird neben geometrischen Strukturen auch die Simulation von Kräften benötigt. Die Kraftentwicklung der extraokulären Muskeln wird durch ein isoliertes Kräftemodell beschrieben, welches für jeden Muskel spezifische Verhaltensmuster vorgibt. Die Struktur des Modells orientiert sich an bereits existierenden Modelltypen für die Skelettmuskulatur. Hierbei wird die Muskelfunktion in passive und aktive Kraftentwicklung eingeteilt. Passive Kräfte entwickeln sich durch Dehnung und Kompression des Muskels, während aktive Kräfte immer ein neurophysiologisches Aktivierungspotential voraussetzen. Die resultierende Funktion aus aktiver und passiver Kraftfunktion simuliert dann die tatsächliche Wirkungsweise des Muskels.

 

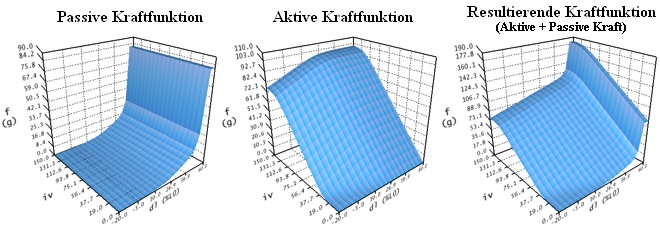
Muskelkräftesimulation des m. rectus lateralis (basierend auf Orbit™, siehe [Miller, 1999])

 

Die in dieser Abbildung dargestellten Funktionen beschreiben die statische Kraftentwicklung eines Muskels bezüglich eines definierten Kraft-Längen-Innervationsverhaltens. Während die passive Kraftentwicklung (f in Gramm) ausschließlich in Abhängigkeit der Längenänderung eines Muskels (dl in Prozent von L0) definiert ist, ist die aktive Kraftfunktion (f in Gramm) zusätzlich von der Innervation (iv) bestimmt. Alle weiteren extraokulären Muskeln sind relativ zu den in dieser Abbildung dargestellten Daten realisiert. Die zugrunde liegenden Daten wurden in Anlehnung an Untersuchungen von Miller und Robinson definiert.

 

Die bisher beschriebenen Modelle der Geometrie und Kraftsimulation werden nun durch die Einführung eines kinematischen Modells miteinander verknüpft. Das kinematische Modell ist für die Übertragung der Kräfte auf das geometrische Modell zuständig. Hierzu wird für jeden Muskel der Rotationswinkel um die geometrische Achse mit der prognostizierten Kraftentwicklung in Relation gesetzt. Das Ergebnis ist dann eine resultierende Rotationsachse mit zugehörigem Rotationswinkel, der eine aktuelle mechanische Wirkungsweise aller sechs Augenmuskeln in einer bestimmten Blickposition beschreibt. Führt man nun eine Rotation des Bulbus in die prognostizierte Richtung aus, verändern sich wiederum die Komponenten der Geometrie und der Muskelkräfte. Durch die geometrische Änderung ergibt sich dadurch eine Veränderung der Muskelwirkungsverteilung und durch die passive Längenänderung der Muskeln verändern sich die Muskelkraftfunktionen und ergeben transitiv eine neue Kräfteverteilung. Dieser Prozess setzt sich solange fort, bis eine stabile Augenposition erreicht werden kann. Eine solche stabile Augenposition ist durch ein Kräftegleichgewicht aller sechs beteiligten Muskeln charakterisiert.

 

Mit Hilfe dieser Simulationstechnik lassen sich die Probleme der Vorwärts- und Rückwärtskinematik lösen. Die Vorwärtskinematik findet bei gegebenen Innervationen für alle sechs Augenmuskeln die resultierende Blickrichtung, wobei die Rückwärtskinematik aus einer gegebenen Blickrichtung wiederum die Innervationen für alle sechs Augenmuskeln ableitet. Kombiniert man nun diese beiden Methoden, so lässt sich ein Test für die binokulare Prüfung von Augenbewegungsstörungen simulieren. Das SEE++ System bildet als eine Möglichkeit den Hess-Lancaster Test ab, in dem es, neben den pathologischen Abweichungen eines Auges, die Normblickpositionen des anderen Auges in anderer Farbdarstellung zeigt.

 

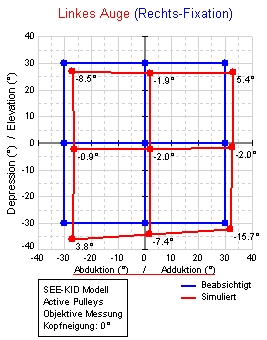
Hess-Test mit Normblickpositionen eines nicht betroffenen

(rechten) Auges (dunkel bzw. blau) und Augenstellungen eines

pathologischen linken Auges (hell bzw. rot).

 

Bei jeder Blickposition eines Auges wird das Innervationsmuster aller Augenmuskeln bei der Fixation mit dem nicht betroffenen Auge bestimmt und an das pathologische Auge weitergegeben (Hering'sches Gesetz), um dessen Blickposition zu bestimmen. Die Innervationen sind nur für die agonistischen Muskeln definiert, die antagonistische Innervation wird durch Anwendung einer reziproken Innervationsfunktion berechnet (Sherrington'sches Gesetz). Das Resultat des Tests lässt sich durch den Vergleich der Normblickpositionen und pathologischen Blickpositionen des geprüften Auges leicht ablesen: Leichte Diplopie in Primärposition, Überfunktion des linken Auges in Depression und Abduktion des rechten Auges, etc.

 

Auf Basis dieser Modelle und deren Parameter wird nun eine pathologische Situation bzw. ein operativer Eingriff simuliert. Die Veränderungen in der Geometrie wirken sich direkt auf das verwendete geometrische Modell aus, indem beispielsweise bei der Versetzung einer Insertion die neuen Insertionskoordinaten direkt übernommen werden und somit eine neue Zugrichtung des Muskels definiert wird. Wie diese Zugrichtung nun im Detail aussieht, ist von der Unterschiedlichkeit der verwendeten Modelle anhängig. So liefert beispielsweise das Fadenmodell eine anatomisch gesehen wesentlich "schlechtere" Darstellung als beispielsweise das Bändermodell von Robinson.