Ziel des Kräftemodells ist es, das Verhalten eines Muskels in Abhängigkeit von seiner Länge und Innervation zu simulieren. Dies wird durch die Definition von drei Kraftfunktionen (Aktive, Passive und Totale Kraft) erreicht. Um das Verhalten eines Muskels zu beeinflussen, um beispielsweise Muskellähmungen (Paresen) oder Überfunktionen zu erzeugen, stellt das Kräftemodell verschiedene Parameter zur Verfügung, die wiederum die Form der Simulationskurven auf bestimmte Art und Weise verändern und so die gewünschte Situation abbilden.

 

Bei der Untersuchung von Muskelkräften unterscheidet man zwei Arten der Kontraktion eines Muskels: Die isotonische Kontraktion und die isometrische Kontraktion. Eine isotonische Kontraktion ist die Messung der Muskellänge bzw. der Muskelverkürzung infolge einer Aktivierung bei konstanter Last (siehe Abbildung A). Im Fall der isometrischen Kontraktion wird die Kraft bzw. die Kraftänderung des Muskels bei konstant gehaltener Länge gemessen (siehe Abbildung B). Der Kontraktionsmechanismus findet auf molekularer Ebene statt und wird durch die so genannte Filament-Gleit-Theorie beschrieben. Dabei verbinden sich Aktin- und Myosinfilamente über so genannte Brückenbildungen und ermöglichen so eine aktivierungsgesteuerte Verkürzung und somit die Entwicklung der Kraft eines Muskels.

 

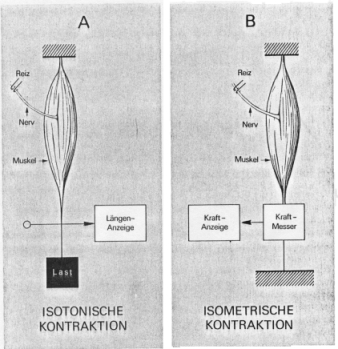
Unterschiedliche Arten der Muskelkontraktionsmessung

 

Generell wird zwischen statischen und dynamischen Eigenschaften eines Muskels unterschieden. Statisches Kraftverhalten wird auch als Kraft-Längenverhalten bezeichnet, wobei man als Ausgangspunkt eine isometrische Kraftmessung durchführt und die erzeugte Kraft in Abhängigkeit der eingestellten (fixen) Länge aufzeichnet. Dynamische Eigenschaften eines Muskels beziehen sich auf Kontraktionsgeschwindigkeiten und werden mit Hilfe von isotonischen Messungen analysiert. SEE++ stellt zur Zeit ein ausschließlich statisches Modell der Kraftentwicklung dar und konzentriert sich auf die Modellierung von Kraft-Längen-Innervationsbeziehungen.

 

Bei der Darstellung der statischen Eigenschaften eines Muskels unterscheidet man wiederum zwischen aktiven (kontraktilen) und passiven (elastischen) Muskelkräften. Aktive Muskelkräfte entstehen durch Aktivierung (Innervation) eines Muskels über das Gehirn, während passive Kräfte die elastischen Dehnungseigenschaften eines Muskels darstellen, die entgegengesetzt zur aktiven Kraft wirken. Führt man nun eine Vielzahl von isometrischen Kraftmessungen bei unterschiedlich eingestellter Länge durch, so ergibt sich eine Kraft-Längenkurve des Muskelverhaltens. Setzt man diese noch in Relation mit dem Aktivierungspotential des Muskels, so erhält man eine dreidimensionale Kraft-Längen-Aktivierungsfunktion. Diese Funktion kann man wiederum in ihre aktiven und passiven Kräfte zerlegen. Man erhält eine aktive und eine passive Kraftkurve, die zusammen der totalen Kraftkurve eines Muskels entsprechen.

 

Die passive Kraftkurve beschreibt die elastischen Kräfte, die der Muskel ausübt, wenn er entsprechend gedehnt oder gestaucht wird. Wenn ein frei liegender, nicht verbundener Muskel ausreichend gedehnt wird, dann wird sich ab einer gewissen Dehnungslänge dieser Muskel nicht mehr wie eine nicht-lineare Feder verhalten, sondern wird sehr schnell steif und nicht mehr weiter dehnbar. Dies wird als so genannte "Leash-Region" bezeichnet und macht sich in einem drastischen Anstieg der passiven Kraft bei erhöhter Dehnungslänge bemerkbar. Umgekehrt, wird ein Muskel in seiner Länge stark zusammengeschoben (gekürzt), so wird er schlaff und kann keine Kraft mehr ausüben. Dies wird auch als so genannte "Slack-Region" bezeichnet.

 

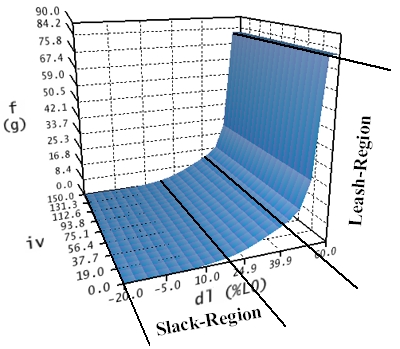
Passive Kraft-Längenkurve

 

 

Wie in der Abbildung ersichtlich, hängt die passive Kraft-Längenkurve nicht von der Aktivierung (iv) eines Muskels ab, da ja ausschließlich passive, elastische Kräfte modelliert werden. Deshalb hat diese Kurve auch in der Längen-Innervationsebene für alle Innervationen die gleiche Form. Die passive Kraftkurve berechnet sich in drei Intervallen (dl < 17%; 17% <= dl <= 40%; dl > 40%), bezogen auf die Längenachse. Als Einheit wird hier Längenänderung in Prozent, bezogen auf die Länge des Muskels im relaxierten Zustand (L0) angegeben. In der ersten Region (dl < 17%) wurde die Muskelkraft manuell langsam auf Null reduziert, während in der dritten Region (dl > 40%) die Kraft bis zu einem Maximum extrapoliert wurde, um den raschen Anstieg der Steifheit des Muskels in der "Leash-Region" zu simulieren. Dazwischen (17% <= dl <= 40%) wird die Elastizität mit einer nicht-linearen Federgleichung berechnet.

 

Die aktive Kraftkurve beschreibt nun die resultierende kontraktile Kraft in Abhängigkeit von Innervation und Länge eines Muskels.

 

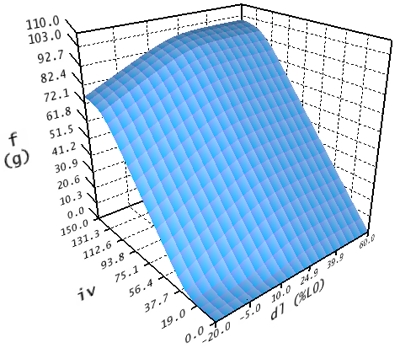
Aktive Kraftkurve

 

Diese Kurve wird auch in drei Abschnitte eingeteilt. Der erste Abschnitt wird innerhalb des Intervalls -20% <= dl <= 45% und 0 <= iv <= 100 berechnet. Der zweite Abschnitt im Bereich -20% <= dl <= 45% und iv > 100 wurde mit Werten aus dem ersten Intervall extrapoliert. Der dritte Abschnitt für dl > 45% wird konstant wie dl = 45% behandelt.

Die totale Kraftfunktion wird nun aus der Summe von passiver und aktiver Kraftfunktion berechnet.

 

Um das Verhalten der Augenmuskeln im Kräftemodell von SEE++ zu verändern, gibt es eine Reihe von Parametern, die ermöglichen, diese Kurven zu manipulieren. Drei globale Parameter werden auf alle sechs Muskeln angewandt und spezifizieren den Aufbau der Kurven im Bereich des Übergang von Slack- nach Leash-Region.

 

•Starrheit (g/% á L0) definiert den Anstieg der Kurve in Richtung der Leash-Region, um so das Verhalten der Muskulatur bei Überdehnung zu approximieren. Als Einheit für den Anstieg werden g pro % auf Basis der relaxierten Muskellänge (L0) verwendet. Wertveränderungen sollten nur in sehr kleinen Bereichen 0 <= x <= 0.9 vorgenommen werden.

•Kraftübergangsskalierung (g) gibt die Form der Kurve im Übergang zur Slack-Region an. Die Einheit in Gramm gibt an, um wieviel die Kurve im Anstieg zum berechneten (zweiten) Intervall gedämpft wird. Je kleiner dieser Wert ist, umso länger bleibt die Kraft bei Dehnung des Muskels Null. Dies entspricht auch einer punktuellen Ausdehnung der Slack-Region.

•Kraftverschiebungsverhältnis (% á L0) verschiebt den berechneten (zweiten) Abschnitt jeder Kurve auf der Längenänderungsachse (dl). Die Verschiebung wird in Prozent von der relaxierten Muskellänge (L0) angegeben.

 

Diese beschriebenen Parameter dienen hauptsächlich für den experimentellen Einsatz im Umgang mit dem Kräftemodell von SEE++. Man sollte diese Werte nur mit größter Sorgfalt verändern, da das Simulationsergebnis stark von diesen Veränderungen beeinflusst wird.

 

Muskelspezifische Parameter

Im SEE++ System werden alle sechs Augenmuskeln nach dem beschriebenen Kräftemodell simuliert. Die Unterschiedlichkeit in der Kraftentwicklung wird durch zwei Skalierungsfaktoren (einen für die passive und einen für die aktive Kraft) definiert, welche die Kraftkurven in Relation zum m. rectus lateralis abändern. Folgende Parameter stehen für jeden Muskel zur Verfügung:

 

•passive Kraft (%/100) skaliert die passive Kraftkurve, um so die elastischen Eigenschaften eines Muskels zu beeinflussen. Eine Verminderung dieses Wertes führt beispielsweise zu einer reduzierten elastischen Kraft, die der Muskel bei Dehnung ausüben kann.

•aktive Kraft (%/100) skaliert die aktive Kraftkurve und simuliert eine Über- oder Unterfunktion des Muskels bezogen auf eine Aktivierung vom Gehirn ausgehend. Ein Wert von 0 würde einer totalen Muskelparese (Totalausfall der kontraktilen Leistung) eines Muskels entsprechen.

•relative passive Kraft (%/100 RL) skaliert die passive Kraftfunktion in Bezug auf den m. rectus lateralis. Verändert man diesen Wert, so stärkt bzw. schwächt man einen Muskel relativ zum m. rectus lateralis; um die passive Kraft relativ zum aktuellen Muskel zu verändern, sollte man den Parameter "passive Kraft" direkt verwenden.

•relative aktive Kraft (%/100 RL) skaliert die aktive Kraftfunktion in Bezug auf den m. rectus lateralis. Verändert man diesen Wert, so stärkt bzw. schwächt man einen Muskel relativ zum m. rectus lateralis; um die aktive Kraft relativ zum aktuellen Muskel zu verändern, sollte man den Parameter "aktive Kraft" direkt verwenden.

 

Bei der Simulation von operativen Eingriffen ist auch die Muskellänge von großer Bedeutung. Die Länge von Muskel und Sehne verändert auch die Art und Weise, wie die Kraftkurven dann vom Simulationssystem "interpretiert werden". Die Veränderung der Muskellänge (dl) wird in den Kraftkurven in Prozenten dargestellt. Als Beispiel sei ein Gummiband mit 10 mm Länge angegeben (relaxierte Länge L0=10 mm). Nimmt man nun dieses Gummiband und dehnt es um 10 mm, so erhält man eine Pfadlänge von insgesamt 20 mm und eine relative Dehnung von 100%. Halbiert man nun dieses Band auf 5 mm relaxierte Länge und dehnt man wieder um 10 mm, so erhält man nun eine relative Dehnung von 200%. Dies würde einer ganz anderen resultierenden Kraft im Kräftemodell entsprechen und zeigt, wie durch Veränderung der Muskellänge das Kraftverhalten eines Muskels beeinflusst werden kann.

 

Das Muskelmodell von SEE+ stellt dazu folgende Parameter zu Verfügung:

 

•Muskellänge (L0) in mm gibt die Länge eines Muskels im relaxierten Zustand, ohne Sehne, an.

•Sehnenlänge in mm gibt die zusätzliche Länge der Sehne an.

•Sehnenbreite in mm gibt die Breite der Sehne an der Insertion an, und wird für die Verteilung der Kraft über die Muskelbreite verwendet.

 

Simuliert man beispielsweise eine Resektion des m. rectus lateralis um 5 mm, so verändert man Muskel- bzw. Sehnenlänge entsprechend. Trennt man die Insertion des m. rectus lateralis ab, schneidet dann 5 mm ab und refixiert den Muskel wieder, so verliert man üblicherweise beim Abtrennen 1 mm und beim Refixieren erneut 1 mm an Muskel- bzw. Sehnenlänge (je nach Operationstechnik können diese Werte variieren und müssen individuell korrigiert werden). SEE++ kann diesen Gegebenheiten natürlich nicht automatisch folgen, somit ist es notwendig in diesem Fall den Muskel um insgesamt 7 mm zu kürzen. Man würde also die Sehnenlänge des m. rectus lateralis von 7.71 auf 0.71 mm verändern. Führt man eine größere Resektion durch, so verliert man die Sehne eines Muskels (Sehnenlänge = 0) und muss die restliche Verkürzung an der Muskellänge vornehmen, also in Summe beide Parameter anpassen. Mit Hilfe der Operationsmethode "Resektion", die man im Dialog "Textuell Operieren" durchführen kann, wird diese Verkürzung der Sehne auf 0 mm und anschließende Verkürzung der Muskellänge bei einer größeren Resektion automatisch vorgenommen.

 

Ein weiterer Parameter, der nur im Orbit-Kräftemodell Anwendung findet, ist die Starrheit des Pulley. Hier wird die passive Bewegung des Pulleys eines Muskels in g/mm limitiert. Veränderungen dieses Wertes, und somit der Bewegung des Pulleys bei Blickpositionsänderungen wirken sich auf die Zugrichtung und somit transitiv auf das Kräfteverhalten des Muskels aus.

 

Innervation der Augenmuskeln

Die Augenmuskeln werden von drei Hirnnerven innerviert. Der Nervus Oculomotorius (III. Hirnnerv) versorgt den m. rectus medialis, den m. rectus superior, den m. rectus inferior und den m. obliquus inferior (außerdem den m. levator palpebrae sowie - mit seinem parasympathischen Anteil - den m. ciliaris und den m. sphincter pupillae). Der Nervus Trochlearis (IV. Hirnnerv) versorgt den m. obliquus superior, der Nervus Abducens (VI. Hirnnerv) den m. rectus lateralis. Jeden Augenmuskel innervieren etwa 1000 Motoneuronen. Die einzelnen Motoneurone verzweigen sich im Augenmuskel und versorgen jeweils ca. 4 bis 40 Muskelfasern. Als motorische Einheit bezeichnet man die Gesamtheit jener Muskelfasern, welche an ein und dasselbe Motoneuron angeschlossen ist.

 

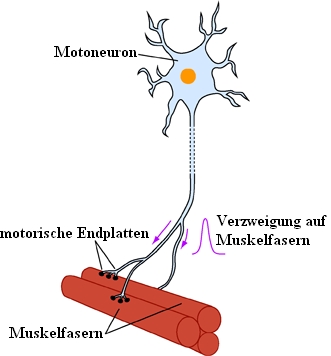
Eine motorische Einheit eines Muskels besteht aus einem

Motoneuron mit allen von diesem Neuron innervierten Muskelfasern

 

Das Gehirn nützt zwei verschiedene Möglichkeiten, um die Zugkraft eines Muskels zu steigern:

 

Motorische Kerne

Die Zellkörper der Motoneuronen liegen in Gruppen vereinigt und bilden die sogenannten Kerne innerhalb des Hirnstamms. Das Kerngebiet der beiden Okulomotoriusnerven liegt paarweise angeordnet im Mittelhirn. Die Anordnung der Teilkerne, die den einzelnen Augenmuskeln zugeordnet sind, ist außerordentlich kompliziert und wurde erst in den letzten Jahren genauer untersucht. Die Zellkörper für den m. rectus medialis, den m. rectus inferior und den m. obliquus inferior liegen ipsilateral (das heißt für das rechte Auge auf der rechten Kernseite). Nur die Zellkörper für den m. rectus superior liegen kontralateral (das heißt für das rechte Auge auf der linken Seite des paarweise angeordneten III. Kernes). Die Nervenfasern für den m. rectus superior kreuzen noch im Okulomotoriuskerngebiet zur anderen Seite. Die Zellkörper für den m. levator palpebrae liegen nahe an der Mittellinie, sowohl ipsilateral als auch kontralateral.

 

Die beiden Trochleariskerne liegen ebenfalls im Mittelhirn, dicht unterhalb des Okulomotoriuskerngebiets. Die Motoneuronen des Nervus Trochlearis entspringen jeweils kontralateral und kreuzen hinter dem Aquädukt, unterhalb der Vierhügelplatte, zur anderen Seite.

Die Abducenskerne liegen in der Brücke und sind mit dem jeweilig ipsilateralen m. rectus lateralis verbunden.

 

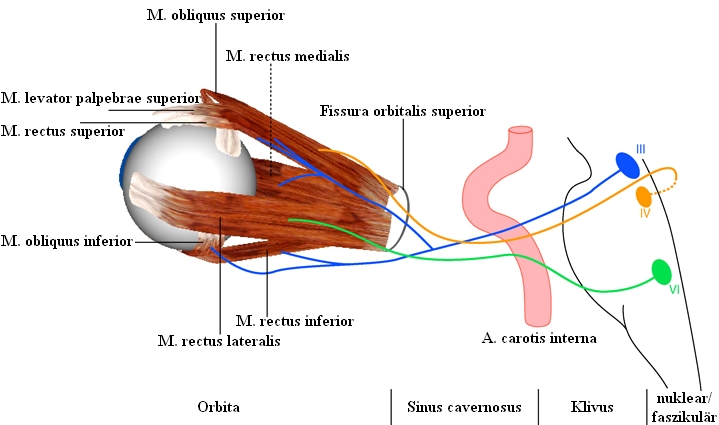
Lage der okulomotorischen Kerne und Verlauf der okulomotorischen Hirnnerven

 

Das SEE++ System enthält keine eigene Simulation des Hirnstamms bzw. supranukleärer Strukturen. Es realisiert aber, auf Basis jedes Auges, eine so genannte Innervationsverteilung, in der, abhängig vom gewählten Auge, die prozentuale Aufteilung der Innervation von den okulomotorischen Kernen auf die jeweiligen Muskeln eingestellt werden kann. Wird eine solche Innervationsverteilung abgeändert, so werden alle Innervationen bezogen auf den betroffenen Muskel für das betroffene Auge prozentual skaliert.

 

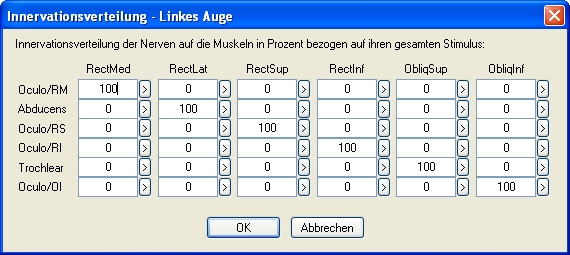
Innervationsverteilung am Beispiel des linken Auges (basierend auf Orbit™, siehe [Miller, 1999])

 

Modifiziert man diese Verteilung der Innervationen, so kann man inter- bzw. supranukleäre Blicklähmungen aber auch beispielsweise Retraktionssyndrome nachbilden. Eine supranukleäre Blicklähmung bei Rechtsblick würde man durch Adaptierung der Innervationsverteilung des Nervus Abducens auf den m. rectus lateralis am rechten Auge, und des Nervus Oculomotorius auf den m. rectus medialis am linken Auge simulieren. Bei einer "einfachen" internukleären Blicklähmung wäre nur ein Auge (Sakkaden) betroffen und somit auch nur die Innervationsverteilung eines Auges zu ändern.

 

SEE++ verwendet ein so genanntes unsichtbares Referenzauge, welches als Basis für die Berechnungen herangezogen wird. Ändert man nun die Innervationsverteilung dieses Referenzauges, so würde man die Veränderung nur auf das beim Blicktest wechselseitig folgende Auge beziehen. Dies ermöglicht beispielsweise die Simulation einer Läsion, die ausschließlich über das folgenden Auge sichtbar wird.