Simulation

SEE++ simuliert mit Hilfe des biomechanischen Modells den binokularen Hess-Lancaster Test. Die Ergebnisse des Tests können in Form von Hess-Diagrammen (Links- und Rechts-Fixation) und in Form einer textuellen Darstellung (Schielwinkeldiagramm) ausgegeben werden.

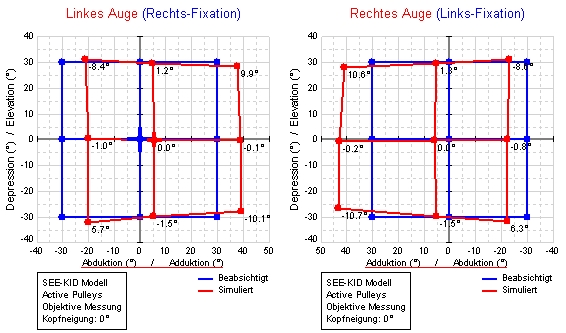
Hess-Diagramme und Schielwinkeldiagramm (Rechts- und Links-Fixation)

Der Unterschied der beiden Darstellungen liegt in der Angabe der Abweichungswerte. Während das Hess-Diagramm einen visuellen Eindruck der pathologischen Situation vermittelt und für beliebig viele Blickpositionen errechnet werden kann, wird das Schielwinkeldiagramm als textuelle Darstellung der Abweichungswerte in den neun Hauptblickrichtungen angegeben.

Im Schielwinkeldiagramm werden für jede Blickrichtung in der Rechts- und Links-Fixation die jeweiligen Abweichungen eingetragen, wobei hier HD für Horizontalabweichung und VD für Vertikalabweichung steht. In den jeweils weißen Feldern wird die Exzyklo- bzw. Inzyklotorsionsabweichung (EX bzw. IN) und die Protrusion in mm (PR; negative Protrusion = Retraktion) angegeben. Alle Angaben außer der Protrusion sind in Grad, wobei für HD und VD eingestellt werden kann, ob die Werte in Grad oder in Prismendioptrien (PD) angegeben werden sollen.

Die Vorzeichen für die horizontale Abweichung sind wie folgt definiert:

•+HD: Zur Nase hin (Adduktion)

•-HD: Von der Nase weg (Abduktion)

Die Vorzeichen für die vertikale Abweichung sind für Rechts- und Links-Fixation verschieden definiert:

Rechts-Fixation

•+VD: Abweichung des linken Auges nach unten (Depression)

•-VD: Abweichung des linken Auges nach oben (Elevation)

Links-Fixation

•+VD: Abweichung des rechten Auges nach oben (Elevation)

•-VD: Abweichung des rechten Auges nach unten (Depression)

Verschiedene Arten von Torsion (Zyklorotation)

Die in den Hess-Diagrammen und im Schielwinkeldiagramm von SEE++ angegebenen Torsionen sind abhängig von der im Programm gewählten Art der Torsionsmessung. Standardmäßig werden die Torsionen so in den Diagrammen eingezeichnet, wie sie bei einer objektiven Messung am Patienten in der Klinik gemessen werden. Objektive Messung bedeutet in diesem Fall, dass die Augenposition inklusive Torsion direkt am Patienten gemessen wird (z.B. mit einem VOG (Video-Okulographie) System oder mit Search Coils) ohne dass der Patient irgendwelche Angaben machen muss. Wird in SEE++ nun auf subjektive Torsionsmessung umgestellt, dann werden die Torsionen so ausgegeben, wie sie der Patient bei einem subjektiven Test (z.B. Tangentenskala, Harms-Wand) angibt. Diese Torsionswerte entsprechen dann der Differenz, die der Patient zwischen dem einen und dem anderen Auge wahrnimmt (Zyklodeviation), da die "normale" Listing'sche Torsion (z.B. 8.2 Grad bei Blick in 30 Grad Adduktion und 30 Grad Elevation), die auch bei einem gesunden Auge vorhanden ist (siehe Listing'sches Gesetz), subjektiv vom Patienten nicht wahrgenommen wird. Um in der Klinik gemessene Torsionswerte mit simulierten Torsionen zu vergleichen muss also die entsprechende Torsionsmessung im Programm ausgewählt werden.

Neben der Listing'schen Torsion berechnet SEE++ auch noch die Gegenrollung, welche bei einer Neigung des Kopfes in Richtung der linken oder rechten Schulter entsteht (VOR - vestibulookulären Reflex). Dazu wird auf Basis der aktuellen Neigung des Kopfes des "virtuellen" Patienten die entsprechende Gegenrollung berechnet und mit der Listing'schen Torsion bzw. mit der Zyklodeviation (abhängig von der gewählten Torsionsmessung) kombiniert. Die so berechnete kombinierte Torsion wird dann in den verschiedenen Diagrammen angezeigt. Im Stateviewer haben sie außerdem die Möglichkeit, die Komponenten, aus denen sich die in den Diagrammen angezeigte Torsion zusammensetzt, einzeln abzulesen.

Simulationsablauf

Manchmal ist es von Vorteil, über die internen Abläufe der Simulation von SEE++ Bescheid zu wissen, wenn man ein Simulationsergebnis interpretiert. Die folgende Abbildung zeigt den schematischen Ablauf der Simulation für den Hess-Lancaster Test, den SEE++ für jede Blickposition aus dem zu fixierenden Blickschema durchführt.

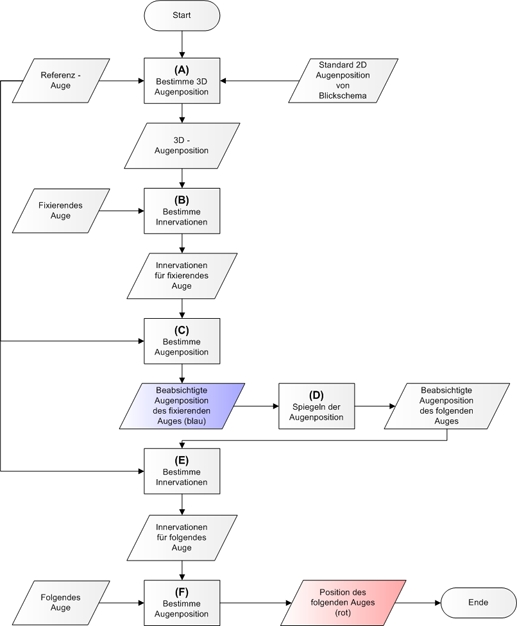
Simulationsablauf beim Hess-Lancaster Test (basierend auf Orbit™, siehe [Miller, 1999])

Ziel ist die Ermittlung der Abweichungen des folgenden Auges von den Fixationspositionen des fixierenden Auges. Dabei können fixierendes und folgendes Auge jeweils vertauscht werden, das heißt entweder ist das rechte Auge fixierend und das linke Auge folgend oder das linke Auge ist fixierend und das rechte Auge folgend. Dies ermöglicht die Berechnung der Rechts- bzw. Links-Fixation.

(A)	Ausgehend von einem gesunden Referenzauge und einer vorgegebenen Fixationsposition wird eine vollständige 3D-Augenposition ermittelt.

Bei der Vorgabe einer Fixationsposition kann natürlich nur Ab-/Adduktion und Elevation bzw. Depression angegeben werden. Die Spezifikation einer Torsion ist nicht möglich, da ein Patient auch üblicherweise nicht bewusst einen bestimmten Torsionswinkel einstellen kann. Dies erfordert die Bestimmung der vollständigen Position des fixierenden Auges und wird errechnet, indem mit Hilfe eines Referenzauges solange Innervationen für Augenpositionen mit Listing'scher Torsion generiert werden, bis die Position des fixierenden Auges mit diesen Innervationen und der gewünschten 2D-Augenposition korreliert.

(B)	Aus der ermittelten 3D-Augenposition und dem fixierenden Auge wird das Innervationsmuster für alle sechs Augenmuskeln berechnet, welches notwendig ist, um das fixierende Auge in die gewünschte Position zu bringen.

(C)

Diese Innervationen werden danach in das Referenzauge gegeben, um dessen Augenposition zu ermitteln. Dies bedeutet, wenn das fixierende Auge pathologisch ist, dass die Ermittlung der Position des Referenzauges eine andere Augenposition ergibt als zuvor. Das Ergebnis dieser Berechnung ist dann die beabsichtigte Fixationsposition des fixierenden Auges.

(D)

In diesem Schritt wird die beabsichtigte Fixationsposition des fixierenden Auges gespiegelt, um die beabsichtigte Position des folgenden Auges zu erhalten. Da man Innervationen nicht spiegeln kann (der kontralaterale Synergist des rechten m.rectus lateralis ist der linke m. rectus medialis und funktioniert möglicherweise nicht identisch), ist dieser "Umweg" über das Spiegeln der Augenposition notwendig. Dies ist möglich, da Ab-/Adduktion und Torsion zwischen den beiden Augen unterschiedliche Vorzeichen besitzen, um dieselbe Richtung anzugeben.

(E)	Nun werden aus der gespiegelten Augenposition die Innervationen des Referenzauges ermittelt, um anschließend die Position des folgenden Auges zu berechnen.

(F)	Die Innervationen des Referenzauges bestimmen nun die Position des folgenden Auges, jene Position, die im Hess-Diagramm als roter Punkt aufscheinen wird.

Literatur

[Brugger, 2000] P.C. Brugger. Der 3D Anatomie Atlas. Weltbild Verlag GmbH, Augsburg, Deutsche Erstausgabe, 2000.

[Buchberger und Mayr, 2000] M. Buchberger und H. Mayr. SEE-KID: Software Engineering Environment for Knowledge-based Interactive Eye Motility Diagnostics (in Englisch). In Proceedings of International Symposium on Telemedicine, Gothenburg, Sweden, 2000.

[Clark et. al., 2000] R.A. Clark, Miller J.M. und J.L. Demer. Three-dimensional location of human rectus pulleys by path inflections in secondary gaze positions. Investigative Ophthalmology & Visual Science, 41(12): 3787–3797, November 2000.

[Demer et. al., 2000] J.L. Demer, S.Y. Oh und V. Poukens. Evidence for Active Control of Rectus Extraocular Muscle Pulleys. Investigative Ophthalmology & Visual Science, 41(6):1280–1290, May 2000.

[Günther, 1986] S. Günther. Die modellmäßige Beschreibung der Augenmuskelwirkung. Diplomarbeit, Universität Hamburg, Universitätskrankenhaus-Eppendorf, Abteilung für medizinische Optik, 1986.

[Kaufmann, 1995] H. Kaufmann. Strabismus. Ferdinand Enke Verlag, Stuttgart, 2. Auflage, 1995.

[Miller 1999] J.M. Miller. Orbit™ 1.8 Gaze Mechanics Simulation Users Manual. Eidactics, Suite 404, 1450 Greenwich Street, San Francisco, CA 94109, USA.

[Miller und Demer, 1996] J.M. Miller und J.L. Demer. Uses of Biomechanical Modeling (in Englisch). In Proceedings of CLADE, Buenos Aires, 1996.

[Miller und Demer, 1999] J.M. Miller und J.L. Demer. Clinical Applications of Computer Models for Strabismus. In eds Rosenbaum, A and Santiago, AP, Clinical Strabismus Management. Philadelphia, W. B. Saunders.

[Pschyrembel, 1994] Pschyrembel. Klinisches Wörterbuch. Nikol VerlagsgmbH, Hamburg, 257. Auflage, 1994.

[Schäffler und Schmidt, 1998] A. Schäffler und S. Schmidt. Biologie, Anatomie und Physiologie. Urban und Fischer Verlag, München, 3., erweiterte Auflage, 1998.

[Yanoff und Duker, 2003] M. Yanoff und J.S. Duker. Ophtalmology. Mosby, London, 2. Auflage, 2003.